Uni-Zirkel PriSMa
Für alle Schüler:innen der Uni-Zirkel PriMa besteht die Möglichkeit in der 5. Klasse und den folgenden Klassen an einer weiterführenden Förderung im Rahmen der Uni-Zirkel PriSMa teilzunehmen. Diese werden einmal im Monat von 16:00 bis 17:30 Uhr (Klasse 5) bzw. von 18:00 bis 19:30 Uhr (ab Klasse 6) angeboten. Die Anforderungen an die Problemstellungen ebenso wie an die Qualifikation der Tutor:innen orientiert sich an dem hohen Qualitätsanspruch der Maßnahme PriMa.
Für viele Schüler:innen stellt der Wechsel zur weiterführenden Schule eine bedeutsame Veränderung dar. Rückmeldungen zur Belastbarkeit der Schüler:innen haben uns darin bestärkt, den einmonatlichen Rhythmus beizubehalten.
Zugrundeliegendes Konzept
Da der Förderung dieselben Ziele zugrunde liegen, wird auch das Konzept beibehalten, die einzelnen Bausteine jedoch altersangemessen ausgestaltet.
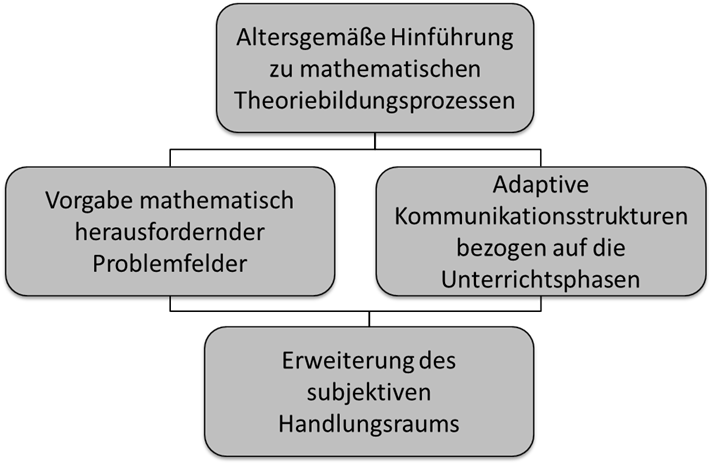
Altersgemäße Hinführung zu mathematischen Theoriebildungsprozessen
Die altersgemäße Hinführung zu mathematischen Theoriebildungsprozessen kann und muss in der Sekundarstufe eine stärkere Hinführung zu mathematisch präzisen Formulierungen und damit auch zur Symbolsprache beinhalten. Darüber hinaus können die Schülerinnen und Schüler zu Verallgemeinerungen auch unter Verwendung von formaler Fachsprache sowie an formale Beweise herangeführt werden, und zwar auf einem höheren Niveau als sie es in der Regel aus der Schule gewohnt sind. Sowohl die Verwendung der Symbolsprache als auch die Aufforderung zu Verallgemeinerungen und Beweisen kann deutlich intensiver erfolgen als im Schulunterricht der jeweiligen Jahrgangsstufe. Das Hereinwachsen in mathematische Denk- und Handlungsweisen („Enkulturation“) zeigt sich u.a. darin, dass die Jugendlichen geradezu ein Bedürfnis zeigen, mathematische Aussagen zu beweisen.
Adaptive Kommunikationsstrukturen bezogen auf die Unterrichtsphasen
Die adaptiven Kommunikationsstrukturen werden wie auch in der Grundschulförderung durchgeführt und können insbesondere für die unterrichtenden Tutor:innen eine Herausforderung darstellen:
- Während der Bearbeitung der Aufgaben durch die Jugendlichen wird das Prinzip der minimalen Hilfe weiterhin angewendet; die Kommunikation mit den Schüler:innen ist explizit auf Verständigung ausgerichtet ohne vorschnelle Interpretationen.
- Während der Plenumsphasen strukturieren die Tutor:innen die Gespräche und fassen sie zusammen. Sie geben Erläuterungen zu den von den Schüler:innen vorgestellten Gedanken unter Zuhilfenahme grundlegender mathematischer Konzepte und Verfahren, die den Schüler:innen teilweise noch unbekannt sind (und ggf. auch gar nicht oder erst später im Schulcurriculum enthalten sind).
Vorgabe mathematisch herausfordernder Problemfelder
Die Vorgabe mathematischer Problemfelder bleibt bestehen. Insbesondere bleibt eine schnell zu lösende Einstiegsaufgabe erhalten, die der Verständnissicherung dient. Dabei kann diese Fragestellung in der Regel deutlich allgemeiner formuliert werden als die Einstiegsaufgaben im Grundschulbereich. Die Teilnehmer:innen haben bereits Herangehensweisen an komplexe Fragestellungen entwickelt und können ihre Beobachtungen und Ideen eigenständig schrittweise verallgemeinern. Auch die anschließenden Fragestellungen werden nur so weit in Teilprobleme vorstrukturiert, wie notwendig ist, um in der begrenzten Zeit Erfolgserlebnisse zu ermöglichen.
Darüber hinaus werden die Jugendlichen immer mehr dazu angeleitet, selbst weiterführende Fragen zu stellen (und natürlich auch zu beantworten), was in der Regel insbesondere auch Verallgemeinerungen und Beweise umfasst.
Erweiterung des subjektiven Handlungsraums
Der Austausch über unterschiedliche Herangehensweisen sowie das Kennenlernen einer anderen Perspektive auf das Problem führen zu einer Erweiterung des subjektiven Handlungsraums und führen so zu einem Lernen von- und miteinander.